まず92号に寄せられた解答の講評をいたします。応募者は問題１に対して１名、問題２に対して１名、あわせて２名でした。問題３には残念ながら解答が寄せられませんでした。紙数の関係で詳しい解説は省きますが、興味のある方は理由を考えたり、さらに発展した問題を作り、自ら解いてみることをお勧めします。

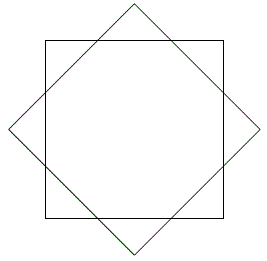
問題１に応募されたのは中学３年のラララ旅人さん（図１）で、等辺16角形になります。線分の本数の２倍の辺でできました。

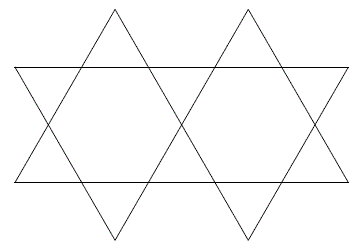
しかし実は、さらに辺の数を増やすことができるのです。図２は８本の線分を使った等辺18角形です。

問題２に応募されたのは小学５年のすみれさんで、「７」という答えでした。正解です。ただ、他にも当てはまる数があります。以下のように考えるとわかりやすいでしょう。３桁の数を２回繰り返して６桁の数を作るということは、その３桁の数に1001をかけることと同じです。２桁の数を３回繰り返して６桁の数を作るということは、その２桁の数に10101をかけることと同じです。１桁の数を６回繰り返して６桁の数を作るということは、その１桁の数に111111をかけることと同じです。1001、10101、111111の最大公約数は91なので、91の約数である「１」「７」「13」「91」が答えです。

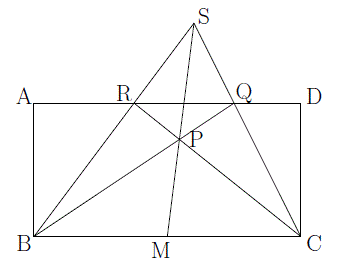
問題３は、たとえば任意の点Ｐと長方形の頂点Ｂ、Ｃを結ぶ直線を引き、直線ＡＤとの交点をそれぞれＱ、Ｒとし、直線ＢＲとＣＱの交点をＳとすると、直線ＰＳは辺ＢＣを２等分します（図３）。

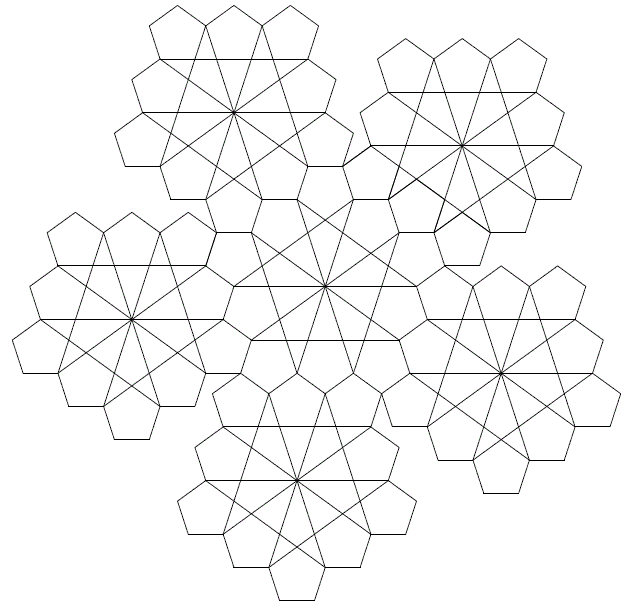
さて、今号では、数学塗り絵を楽しんでいただきたいと思います。近年の小学校の算数の学習指導要領でも敷き詰め模様により図形の美しさを味わうべきことが述べられるなど、注目されています。正多角形のうち、平面を敷き詰めることができるのは正三角形、正方形、正六角形に限られますが、今回は正五角形を基調としたデザインを作ってみました。みなさんも直線や曲線を組み合わせて作ってみませんか？

塗り絵をお寄せください

下のデザインをデータとして保存し（画像の上でマウスを右クリックし、「名前をつけて画像を保存」を選んでください）、お絵かきソフトなどで自由に色を塗ったもの、または新しい塗り絵のデザインを、住所、氏名（紙上での仮名を希望される方は（仮名：○○）と追記してください）、年齢（または学年）を添えて、申し込みフォームからお送りください。十月以降に鑑賞会を開き、優秀作品を選びたいと思います。