日本には和算の伝統がありますが、古くからお寺や神社に、額や絵馬の形で和算の問題や解法を記したものを奉納するという習慣がありました。蓬莱町にもお寺さんが多いので、奉納された算額があったかもしれません。

算額の中には、厳しく身分や男女を分けていたはずの江戸時代に、数学塾では男女が同席し、身分や歳に関係なく自由に話し合うようすが描かれているものもあります。このように身分制度から自由になれる異質の空間だったことが、江戸時代に民間の塾が繁栄した一因だったと、四日市大学関孝和数学研究所長、京都大学名誉教授の上野健爾氏は述べています。

そこで、本コーナー「蓬莱算額」を始めます。このコーナーを通じて、算数や数学を学び探求する喜びや、数理的なものの考え方の価値を伝え、数学のことだけでなく世の中の課題などもじっくり考え抜く人を育てることに貢献できればと思います。また、蓬莱町の古い文化の掘り起こしのきっかけの一つになればとも思います。

問題を３題ほど作りましたので、よろしければ挑戦してみてください。問題の意味は中学生くらいに（可能なら小学校高学年くらいにも）理解できて、大人も楽しめるようなもの、という方針で作ってみましたが、いかがでしょうか。次号で正解者の発表と簡単な解説をいたします。また、五月以降に解説会を計画しており、別途ご案内いたします。

算額は二十一世紀の現在も全国の愛好家によって作られ、奉納されているようです。関心のある方が集まれば、蓬莱町でも算額を作るイベントを企画してもよいかもしれません。この連載の「蓬莱算額」というタイトルはここから生まれました。

次号からは、とりわけ文京区に関わりのある和算や算額の話題も紹介していきたいと思います。

参考文献

• 上野健爾(2017) 『和算への誘(いざな)い――数学を楽しんだ江戸時代』平凡社

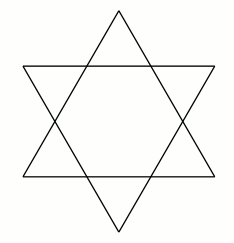
問題１ 下の図の左は、 外側の辺をたどると等辺10角形(どの辺の長さも等しい10角形) になるように５本の線分を引いたもの、下の図の右は、外側の辺をたどると等辺12角形になるように６本の線分を引いたものです。では、８本の線分を使い、なるべく辺の数が多い等辺多角形を作ってください。できた方は線分の数を変えたものも試してみてください。

問題２ ３桁の好きな数を思い浮かべてください。その数を２回繰り返して６桁の数を作ってください。また、２桁の好きな数を思い浮かべてください。その数を３回繰り返して６桁の数を作ってください。さらに、１桁の好きな数を思い浮かべてください。その数を６回繰り返して６桁の数を作ってください。たとえば、３桁の数として「１３５」を思い浮かべた場合は「１３５１３５」、２桁の数として「２８」を思い浮かべた場合は「２８２８２８」、１桁の数として「４」を思い浮かべた場合は「４４４４４４」ができます。このようにして作った数は、必ずある共通の数の倍数になっています。その「ある数」とは何でしょうか。

問題３ 長方形があるとして、その長方形のどれか１辺を、定木だけを使って２等分できるでしょうか。なお、定木でできることは、２点を通る直線を引くことだけで、長さを測ることはできません。また、コンパスは使えません。

下の「「蓬莱算額」その1(2018年3月25日号)解答エントリー」をクリックし、解答をお送りください。1問だけでもいいですし、部分的な解答でもかまいません。

また、「蓬莱算額」へのご意見 もお寄せください。